Traditional Names and Modary Names

This article is not yet centered for mobile-phone browsing.

Near the beginning of the Middle Ages, the term 'Mode' referred to any of the 7 unique scales that can be recognized of the Major Scale; melodies could be created around any one of these 7 root-notes while such root-notes would stay tonally emphasized by the melody throughout the duration of the passage. The respect found of these primary modes is perhaps one of the most important milestones in harmony theory's history.

Present Modary Name:	Abbreviation:	Technical Name:	Traditional Name:
	x	x
	x	x
Main Red	MR	Lydian Mode
	x	x
	x	x
Main Orange	MO	Ionian Mode	Major Scale
	x	x
	x	x
Main Yellow	MY	Mixolydian Mode
	x	x
	x	x
Main Green	MG	Dorian Mode
	x	x
	x	x
Main Blue	MB	Aeolian Mode	Natural Minor Scale
	x	x
	x	x
Main Indigo	MI	Phrygian Mode
	x	x
	x	x
Main Violet	MV	Locrian Mode
	x	x

Inevitably harmonization developed further, and songs became more sophisticated while harmony theory tried to stay in par with the new songs. We may keep in mind that equal-temperament, which is the foundation of the chromatic medium that we use today, was hardly dreamed of; the harmonic series was considered as scientific as well as so divine that any chromatic scale should adhere to it. Music theory and composers had difficulty denying that there had to be some compromise between science and tradition; and there was no scientific justification of the math of equal-temperament until the 16th century.

Later, around the time that equal-temperament was being discussed along with great efforts to compromise between equal-temperament and the harmonic series, classical harmony was frequently utilizing variances of the natural minor scale, namely: the harmonic minor scale and the melodic minor scale.

Now that equal-temperament is a part of our modern scientific understanding, we are beginning to accept the fact that both the harmonic minor scale and the melodic minor scale also each have seven modes.

Of Melodic Minor; common in Jazz Harmony:

Present Modary Name:	Abbreviation:	Estimated Name:	Traditional Name:
	x	x
	x	x
Sub Red	UR	Lydian #5 Mode	Lydian Augmented Sc.
	x	x
	x	x
Sub Orange	UO	Lydian b7 Mode	Acoustic Scale
	x	x
	x	x
Sub Yellow	UY	Ionian b3 Mode	Melodic Minor Scale
	x	x
	x	x
Sub Green	UG	Mixolydian b6 Mode	Major-Minor Scale
	x	x
	x	x
Sub Blue	UB	Dorian b2 Mode
	x	x
	x	x
Sub Indigo	UI	Aeolian b5 Mode	Half-Diminished Scale
	x	x
	x	x
Sub Violet	UV	Superlocrian Mode	Altered Scale
	x	x

Of Harmonic Minor; common in Classical Harmony:

Present Modary Name:	Abbreviation:	Estimated Name:	Traditional Name:
	x	x
	x	x
North Red	NR	Lydian #2 Mode
	x	x
	x	x
North Orange	NO	Ionian #5 Mode
	x	x
	x	x
North Yellow	NY	Dorian #4 Mode	Ukrainian Dorian Scale
	x	x
	x	x
North Green	NG	Aeolian #7 Mode	Harmonic Minor Scale
	x	x
	x	x
North Blue	NB	Mixolydian b2b6	Phrygian Dominant Sc.
	x	x
	x	x
North Indigo	NI	Phrygian b5 Mode
	x	x
	x	x
North Violet	NV	Superlocrian bb7 Mode
	x	x

The Modary™ System provides color labeling for each of its 119 qualified modes; these modes are collectively members of 17 unique spectrums. So in this system the modes can be labeled briefly with the abbreviation of their spectrum followed by abbreviation of their color. The reason for the particular color assignment of the system is made more clear in the next article which explains the anatomy of this modal system.

The Spectrum of the system that is spatially opposite to the North Spectrum is introduced here, along with that spectrum's most melodic mode, SY. Later it will become evident that the spatial opposition between spectrums is not directly related to the major versus minor polarity as it seems to be in this example. The color green will always be found at the center of its spectrum, and the color yellow can only be its opposite when the entire structure of the underlying chords are being considered:

Present Modary Name:	Abbreviation:	Estimated Name:	Traditional Name:
	x	x
	x	x
North Green	NG	Aeolian #7 Mode	Harmonic Minor Scale
	x	x
	x	x
South Yellow	SY	Ionian b6 Mode	Harmonic Major Scale

The difference between a mode and a scale is explained by their respective definitions: A scale is the fixed intervallic form of any set of notes within an octave, while a mode is defined more specifically as the fixed intervallic form of a qualified set of only 7 of the 12 chromatic pitches available within an octave. The qualifications necessary to the definition of 'mode' are partly provided by this new modal system.

Here is a list of some more of the system's modes which are already being recognized in the art as valid scales:

Present Modary Name:	Abbreviation:	Estimated Name:	Traditional Name:
	x	x
	x	x
Reflective Green	RG		Double Harmonic Scale
	x	x
	x	x
Reflective Yellow	RY		Hungarian Minor Scale
	x	x
	x	x
East Green	EG	Aeolian #4 Mode	Gypsy Scale
	x	x
	x	x
East Blue	EB	Phrygian #7 Mode	Neapolitan Minor Sc.
	x	x
	x	x
Dissolving Green	VG		Neapolitan Major Sc.
	x	x
	x	x
Dissolving Blue	VB		Major Locrian Scale
	x	x
	x	x
Sugar Blue	GB		Persian Scale
	x	x

It is evident, in reference to the listing under 'estimated name', that there is difficulty in using the labels of modes as a description of their physical structure; although, it is true that there are various patterns that are recognized when comparing the modes. Having more than one name for the same mode does not present a problem; a problem with communication occurs when one word applies to several vastly different things.

For the Modary System to function, there is no requirement to use only one name for each of the various modes. This system introduces new modal-scales which are necessary for the system to function, and the functionality of the system allows for the tonal foundations that exist between various scales to be recognized, thereby also providing an explanation of the harmony-foundation of some popular scales which contain more than 7 notes. For example, the Flamenco Scale is shown through this system to simply be the bimodal combination of the Phrygian Dominant Scale [NB] and the Phrygian Mode [MI].

Present Modary Name:	Abbreviation:	Estimated Name:	Traditional Name:
	x	x
	x	x
Main Indigo	MI	Phrygian Mode
	x	x
	x	x
North Blue	NB	Phrygian #3 Mode	Phrygian Dominant Sc.
	x	x
	x	x
Multimodality	MI + NB	N/A	Flamenco Scale

In this system, the modes North Blue and Main Indigo easily form the popular Flamenco Scale which has 8 notes rather than the usual 7; the combination of these two modes is made possible since both of these elementary modes exist at 100% within the same column on the system's Map of harmony. It's practically quite as simple as that. The complexity of the system comes in when we begin to use the map's values to guide us during modulation. Otherwize, many other possible multimodal scales can be made by following this same rule.

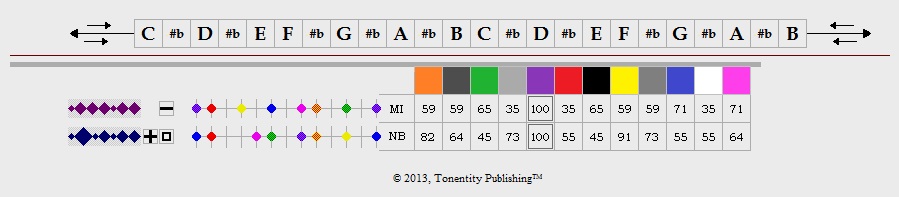
In this system, the modes North Blue and Main Indigo can form the popular Flamenco Scale which has 8 notes rather than the usual 7; the combination of these two modes to form an 8-note scale is made possible due to the fact that both of these elementary modes exist at 100% within the same column on the system's Map of harmony. It's practically quite as simple as that. The complexity only comes in when we begin to consider all of the other possible scales that could be made by following this same rule.


Spectrum Background	Map of Music Harmony

Helpful insight for the above article was provided by the following:

All-Piano-Scales.Com: Musical-Modes

Wikipedia: List of Musical Scales and Modes

Other knowledge about this subject is welcomed and respected.